仕事関数を「電子を固体内部から放出させるのに必要な最小のエネルギー」と定義しましたが、これは、バルク項と表面項の和として表されます。
仕事関数=バルク項+表面項
バルク項は物質によって決まります。表面項は表面の状態、つまり原子配列、構造、吸着物質などにより変化します。
バルクとは塊の事で、ここでは表面に対して固体内部を表す言葉として使います。
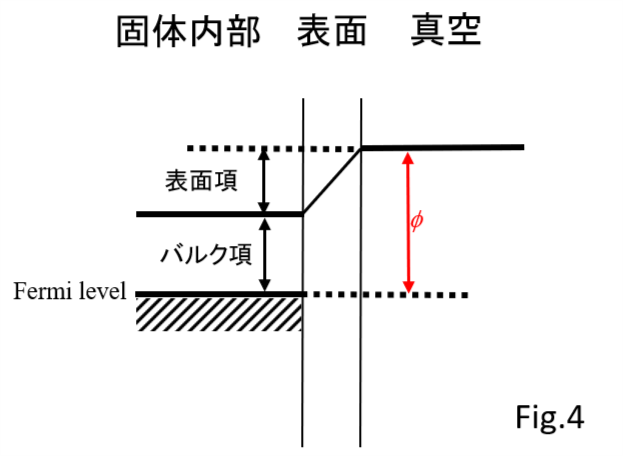
Fig.4 は金属の内部と表面、および表面近傍の真空中における電子状態図です。固体内のフェルミ準位の電子を真空の真空準位まで励起させるためには仕事関数Φのエネルギーが必要です。
この仕事関数Φはバルク項(フェルミ準位と、表面が無い固体内部の真空準位とのエネルギー差)と表面項(表面の影響による真空中での真空準位と、固体内部での真空準位とのエネルギー差)との和になります。
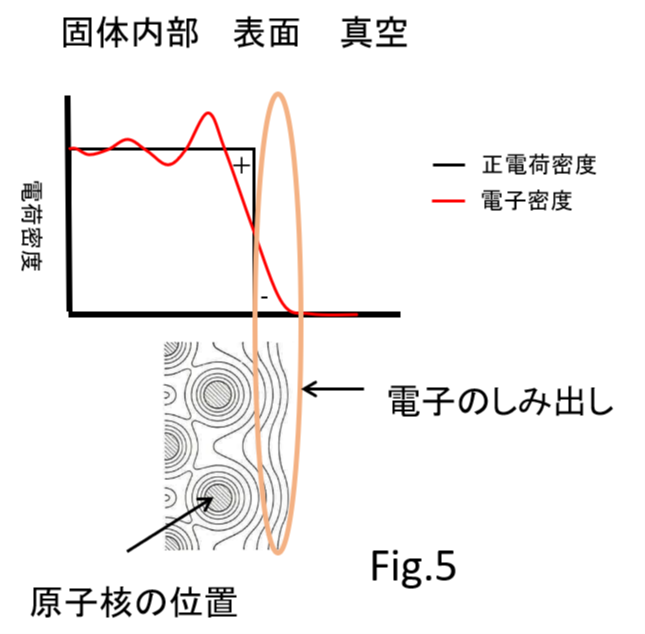
Fig.5 の上側(a)は金属の内部と表面、および表面近傍の真空中における電荷密度を表す図です。
下側(b)は金属の表面での原子核の周辺の電子密度を等高線で表した図です。
固体内部では原子核による正電荷と電子による負電荷が釣り合っています。真空には正電荷も電子も有りません。正電荷は原子核に起因するので、表面内部に固定されています。しかし、電子は動く事ができるので、真空側にしみ出します。
このため、電子がしみ出した分、固体内部は正に偏ります。つまり、内部から取り出される電子は(電子のしみ出しが無い場合に比べてしみ出しがある場合には)固体内部の正への偏りの分だけ余分なエネルギーを必要とします。この余分なエネルギーが「表面項」です。
金属表面での電子のしみ出し度合いは、金属結晶の面方向により異なります。
原子レベルでは表面は平坦ではなく、原子がある場所は盛り上がり、無い場所はへこんでいます。
電子は盛り上がったところからへこんだところへ流れ込み表面をできるだけ平坦にしようとします。
これを「ならし効果」と呼びます。
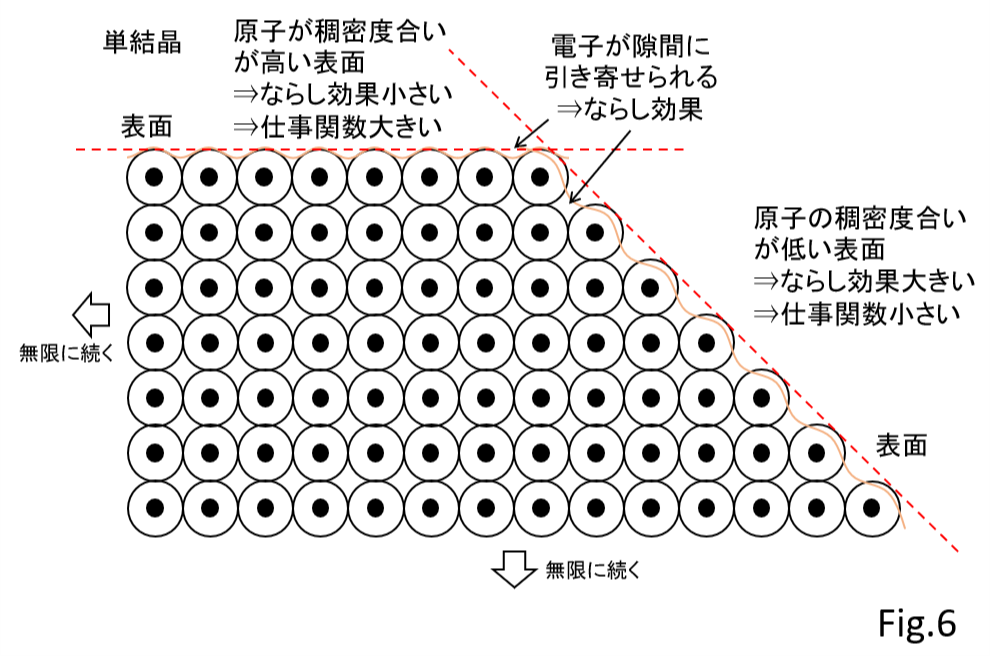
ところで、原子が規則正しく並んだ金属単結晶では、図の様に単結晶を切る面によって原子の隙間が小さい(稠密度合いが高い面)と、原子の隙間が大きい(稠密度合いが低い)面があります。
原子の稠密度合いが低い隙間の多い表面では、ならし効果により電子は金属側に引き寄せられますから、ならし効果が大きい面では電子のしみ出しによる内部の正電荷の増大がその分緩和され仕事関数は比較的小さくなります。
Table.1 単結晶表面での仕事関数の測定値
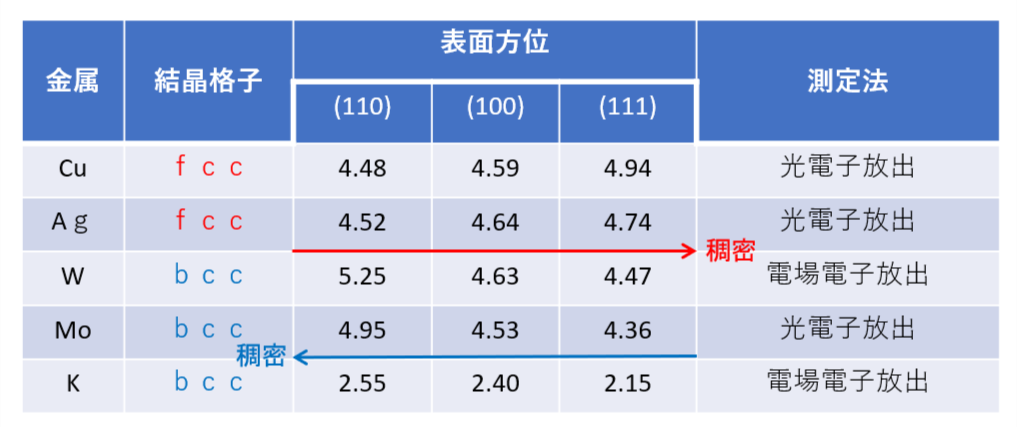
この表は単結晶表面での仕事関数の測定値の比較表です。
CuやAgのように結晶格子がfccの金属の場合、表面方位が(110), (100), (111)の順に稠密度が高くなります。
このとき、電子のしみ出しはこの順番に少なくなり、仕事関数は大きくなります。
W,Mo,Kのように結晶格子がbccの金属の場合、表面方位が(110), (100), (111)の順に稠密度が低くなります。
このとき、電子のしみ出しはこの順番に多くなり、仕事関数は小さくなります。